KelpNetでCNN
今回は、KelpNetでCNN (Convolutional Neural Network) を学習していきます。CNNは、日本語では畳み込みニューラルネットワークと呼ばれています。畳み込みニューラルネットワークとは、畳み込み層やプーリング層を用いて構成されたニューラルネットワークのことです。また、最近のネットワークでは、プーリング層が無い畳み込みニューラルネットワークも多いです。
畳み込みニューラルネットワークは、画像を入力とする場合に多く用いられています。最近は、画像だけでなく音声や自然言語(日本語や英語など)を扱う場合にも用いられることが多いです。
この記事は、ニューラルネットワークの基礎・KelpNetの概要を理解している方を対象にしています。この記事を読み終わるころには、「全結合層の問題」「畳み込み層の概要・特徴・設定・数式での表現」「KelpNetで畳み込み層を用いる方法」「プーリング層の概要・設定」「KelpNetでプーリング層を用いる方法」が分かるようになっており、説明もその順に行っています。
ニューラルネットワークの基礎・KelpNetの概要は、それぞれ以下の記事で紹介しています。
全結合層の問題
全結合層とは、ある層の各ユニットが前の層の全てのユニットと結合している層のことです。これまでの記事では、この全結合層を扱ってきました。
しかし、画像などの高次元のデータに対して全結合層を用いるとパラメータ数(重みの数)が膨大になってしまい、学習が困難になってしまいます。
例として、512×512のサイズのRGB画像を入力とする場合を考えてみます。入力画像の画素数は512 × 512 = 262,144個です。また、1画素につきR・G・Bの3つの色の値を持つため、512×512のサイズのRGB画像は262,144 × 3 = 786,432個の値を持つことになります。これらの値を入力として、次の層を仮に1,024個のユニットからなる層だとすると、パラメータ(重み)の個数は786,432 × 1,024 = 805,306,368個となります。

そこで、画像特有の特徴を考慮してネットワークの構造に制約をかけることによってパラメータ数を減らし、学習を簡単にしたものが畳み込み層です。
畳み込み層の概要
はじめに、畳み込み層の概要を紹介します。全結合層では入力をベクトルとして扱いましたが、畳み込み層では、入力を高さ×幅の行列を基本単位として扱います。また、この行列のことをチャンネルと呼びます。例えば、512×512のサイズのRGB画像は各画素につきR・G・Bの3種類の色を持つため、512×512のサイズのチャンネルが3枚あると考えることが出来ます。
畳み込み層では、下図のように入力チャンネルに対してフィルタをかけることで出力チャンネルを得ます。このフィルタの値が重みの役割を果たしており、学習によって調節されます。

畳み込みは、実際には以下のように左上から順にフィルタをかけることによって行います。入力値に対応するフィルタの値を掛けることによって、出力値を求めます。
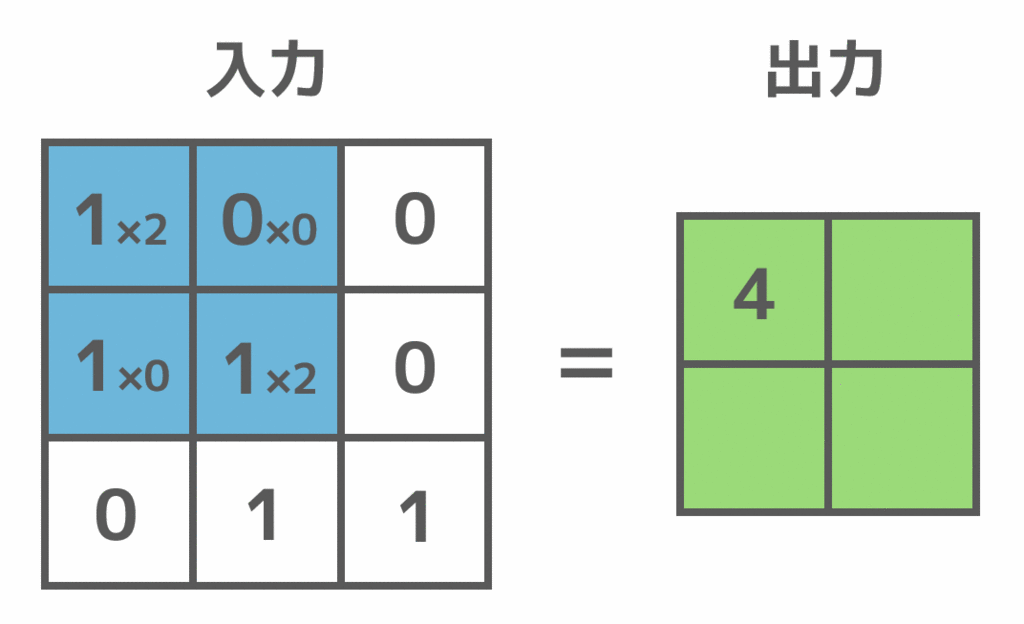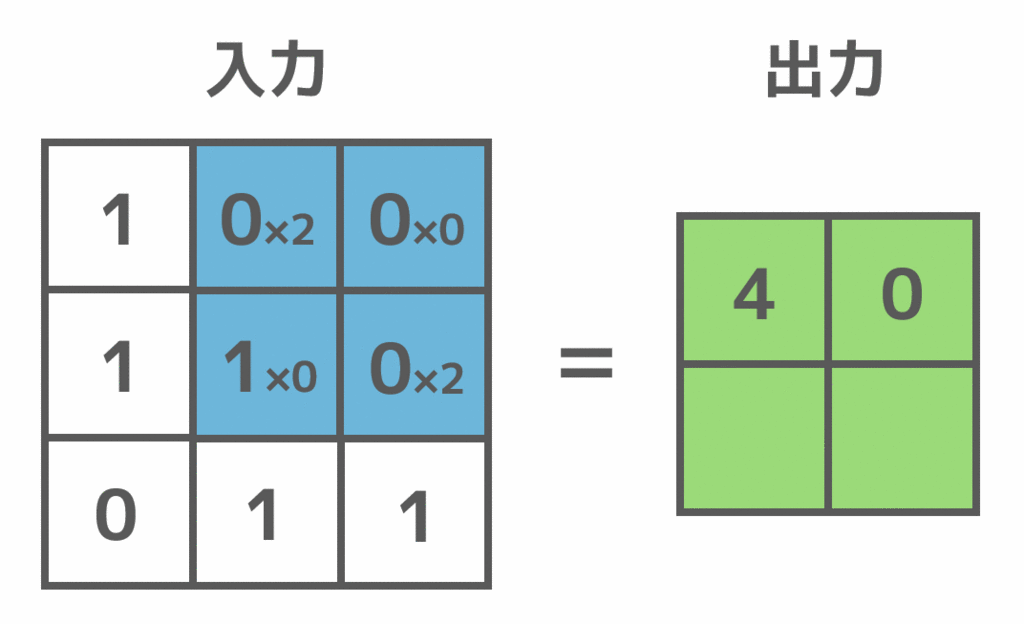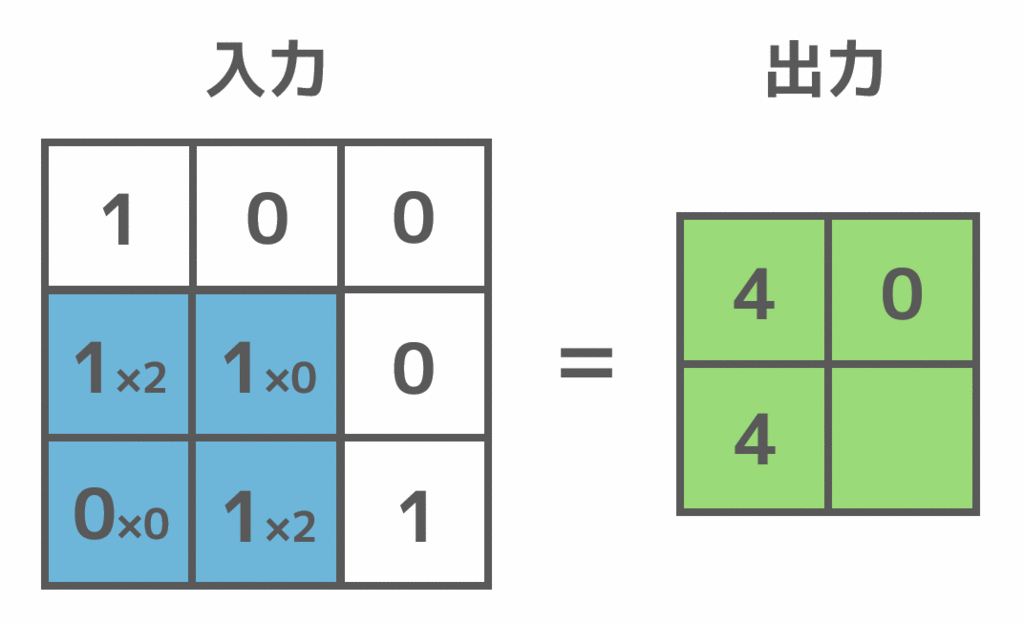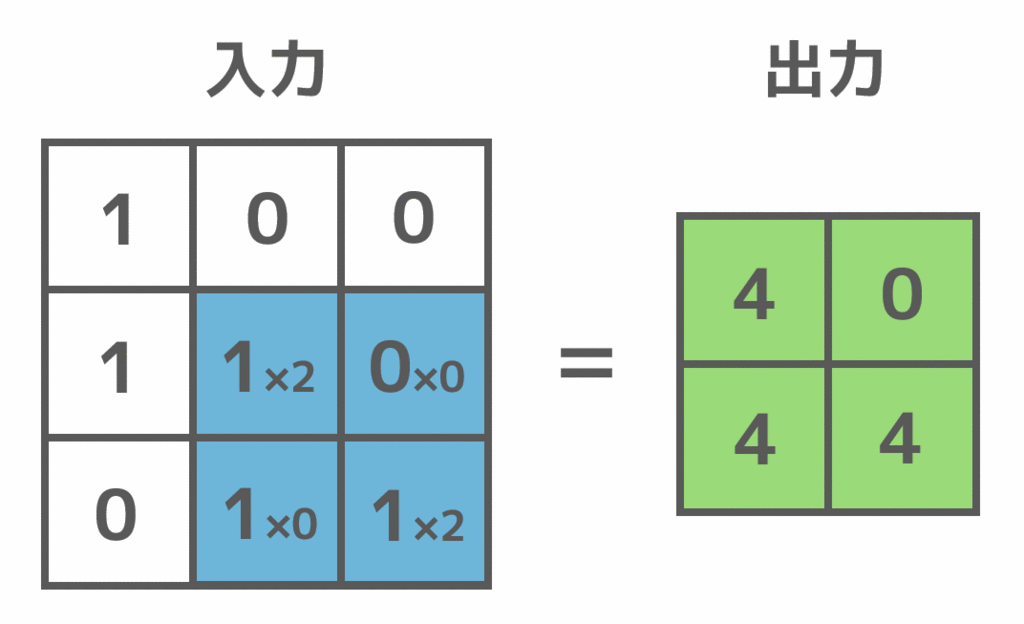
畳み込み層の特徴
畳み込み層は、局所的受容野と重み共有という2つの特徴を持っています。これらの特徴によってパラメータ数が大幅に削減されており、全結合層では困難であったサイズの大きい画像での学習を可能にしています。以下では、その2つの特徴について説明します。
局所的受容野
受容野とは、あるニューロン(ユニット)へ入力を行う領域のことです。全結合層では、各ユニットは前の層の全てのユニットから入力を受け付けるため、受容野は前の層の全てのユニットとなります。しかし、受容野が広ければ広いほど多くのユニットと結合するため、多くのパラメータ(重み)が必要となります。

そこで、画像の「近隣の画素とは関係性が強いが、遠くなるほど画素同士の関係性が弱くなる」という特徴について考えます。下図は、その特徴を図で説明したものです。ゾウの牙は近隣のゾウの鼻とは強い関係性を持ちますが、遠く離れたパンダの耳とは関係性が弱いことが分かります。
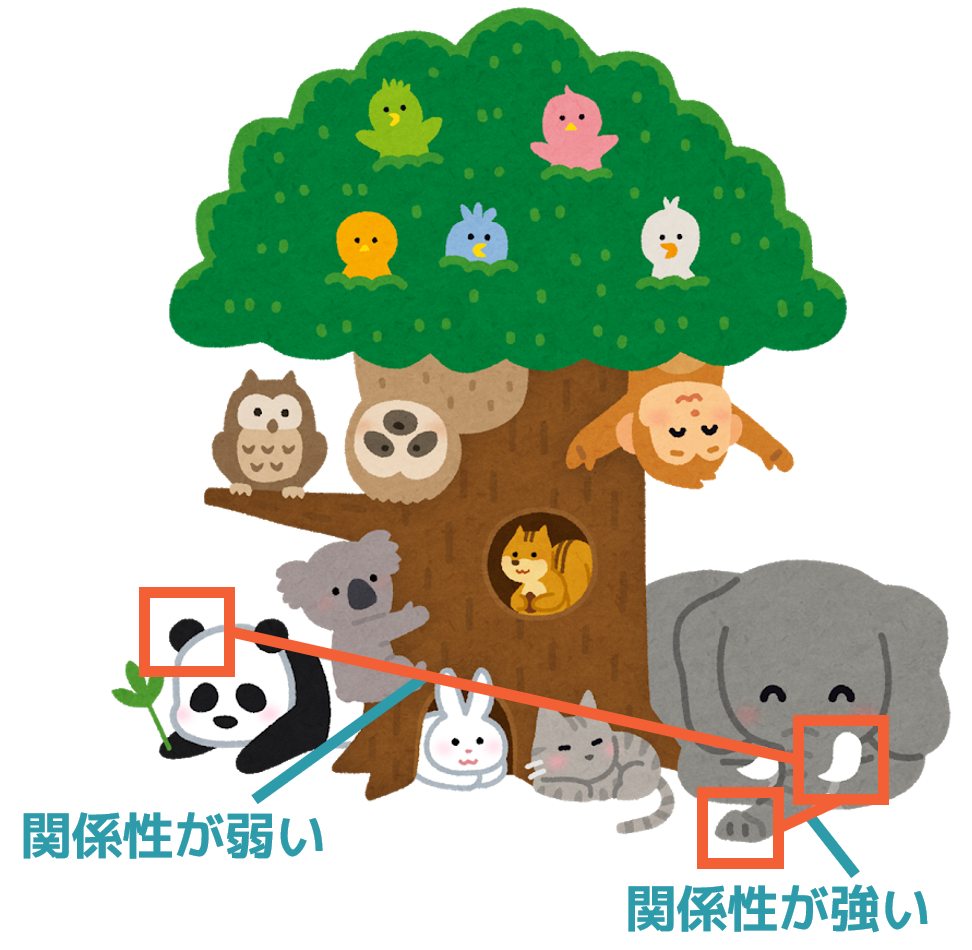
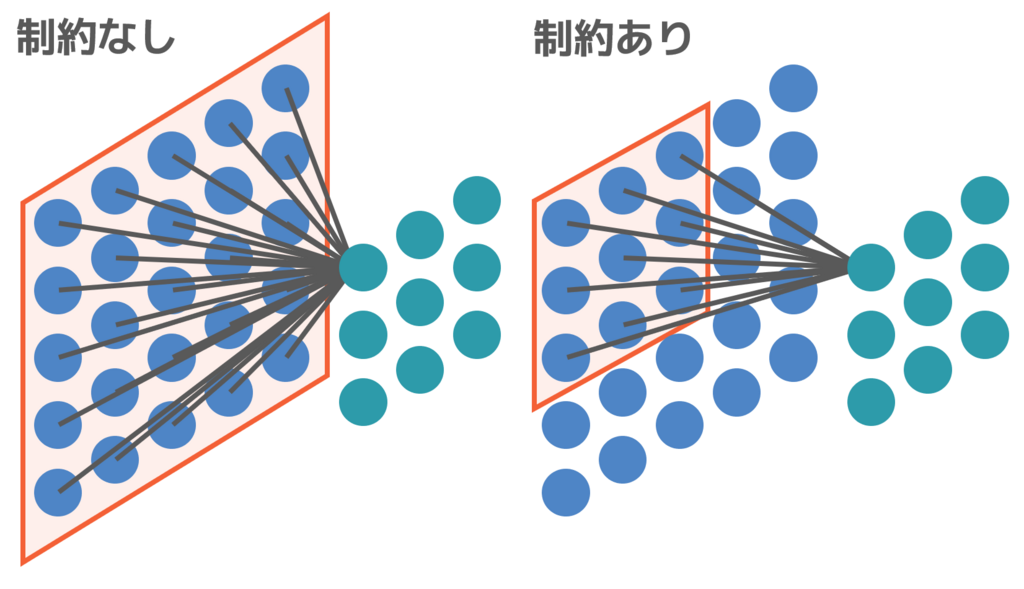
そこで、受容野に「近隣の画素とのみ結合する」という制約を加えます。これによって、関係性が強い近隣の画素とのみ結合することになり、パラメータ数が大幅に削減されます。このように、受容野に「近隣の画素とのみ結合する」という制約を加えるのが、局所的受容野という考え方です。

実際に比較すると「近隣の画素とのみ結合する」という制約を加えるか加えないかで、結合(重み)の数が大きく削減されることが分かります。
重み共有
畳み込み層は、局所的受容野だけでなく重み共有という工夫も行うことで、さらにパラメータ数を減らしています。重み共有は、画像の「ある位置で重要な特徴は、他の位置でも重要である可能性が高い」という特徴を利用しています。
例として、画像の中に猫がいるかどうかを学習するとします。その際、下図のように様々な位置に猫がいることが考えられます。

この場合、各位置にいる猫について別々のフィルタ(重み)で学習しなくてはいけないため、学習が困難になってしまいます。

そこで、猫がどこにいても同じように認識出来るようにすることを考えます。このように、「位置に関係なくある特徴を認識可能であること」を、位置不変性といいます。
ここで、位置不変性を持てないのは「各位置で別々の重みを持つため」でした。そのため、「1つの畳み込み層の中では、位置によって別々のフィルタ(重み)を用いるのではなく、1つのフィルタ(重み)を共有する」というのが重み共有の考え方です。

このように、重みを共有することで位置不変性を持つことが出来ます。また、重み共有を行うことでこれまで、フィルタをかける枚数分のフィルタが必要でしたが、フィルタ(重み)を共有することで1枚で済むためパラメータ数(重みの数)を大幅に削減することが出来ます。
畳み込み層の特徴まとめ
これで、畳み込み層の特徴である「局所的受容野」と「重み共有」について説明しました。まとめると以下のようになります。
局所的受容野
- 問題:受容野が広すぎるとパラメータ数が膨大になってしまう。
- 特徴:近隣の画素とは関係性が強いが、遠くなるほど画素同士の関係性が弱くなる。
- 解決策:関係性が強い近隣の画素のみを受容野とすることで、パラメータ数を削減する。
重み共有
- 問題:位置によってフィルタ(重み)が違うため、各位置について別々に学習しなくてはいけない。
- 特徴:ある位置で重要な特徴は、他の位置でも重要である可能性が高い。
- 解決策:1つの畳み込み層では、1つのフィルタ(重み)を共有する。
また、図にまとめると以下のようになります。局所的受容野を適用することによってフィルタの大きさを小さくし、重み共有によってフィルタの種類を減らせていることが分かります。このように、局所的受容野と重み共有によってパラメータ数(重みの数)を減らすことが出来ます。
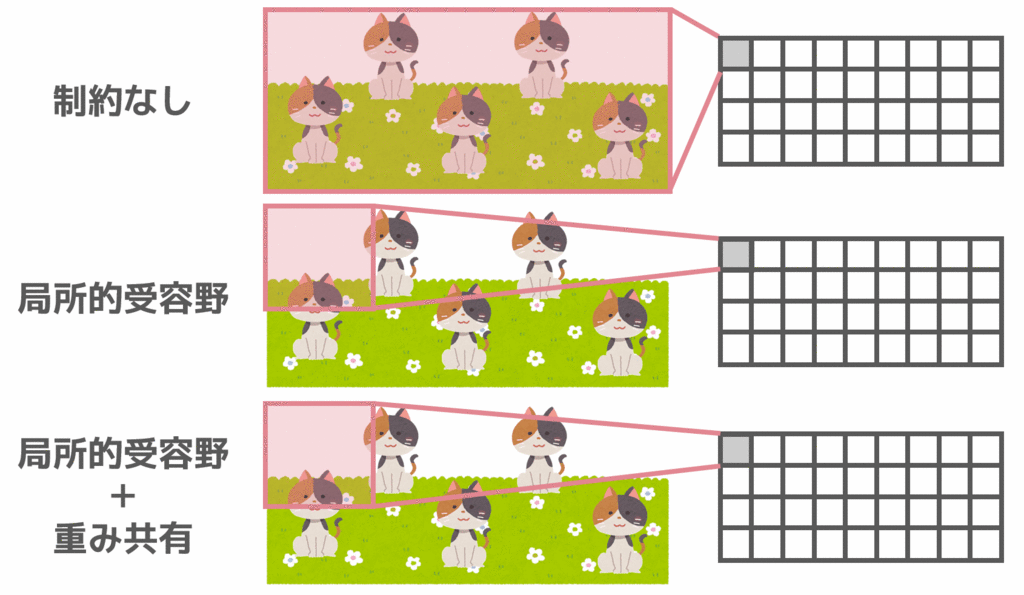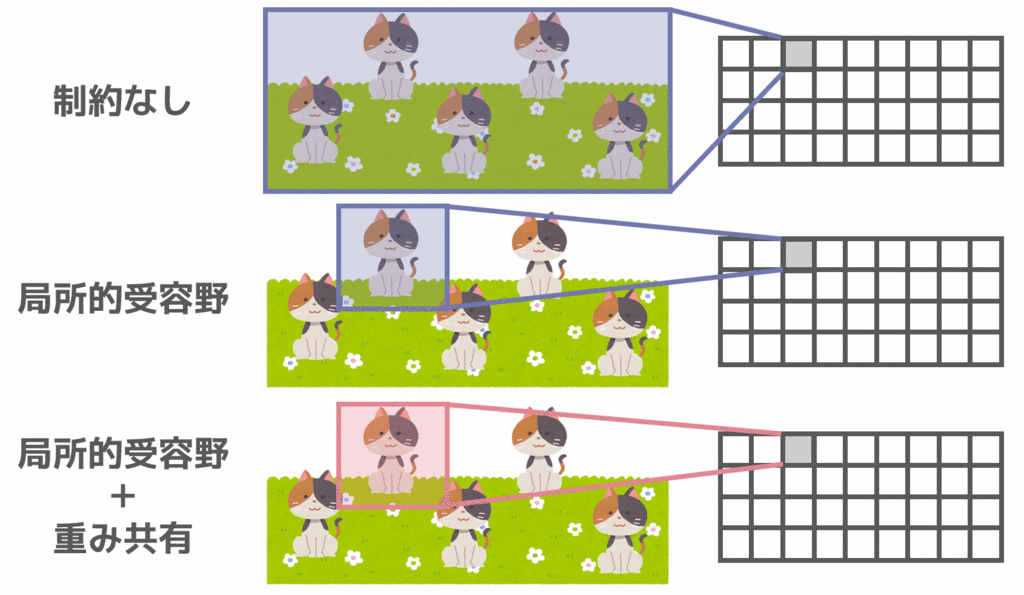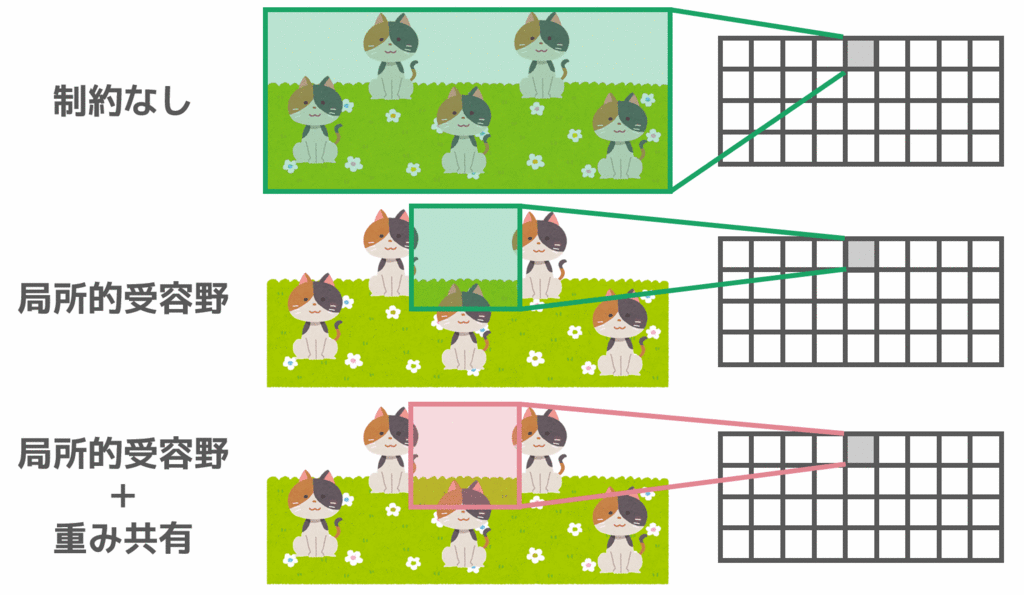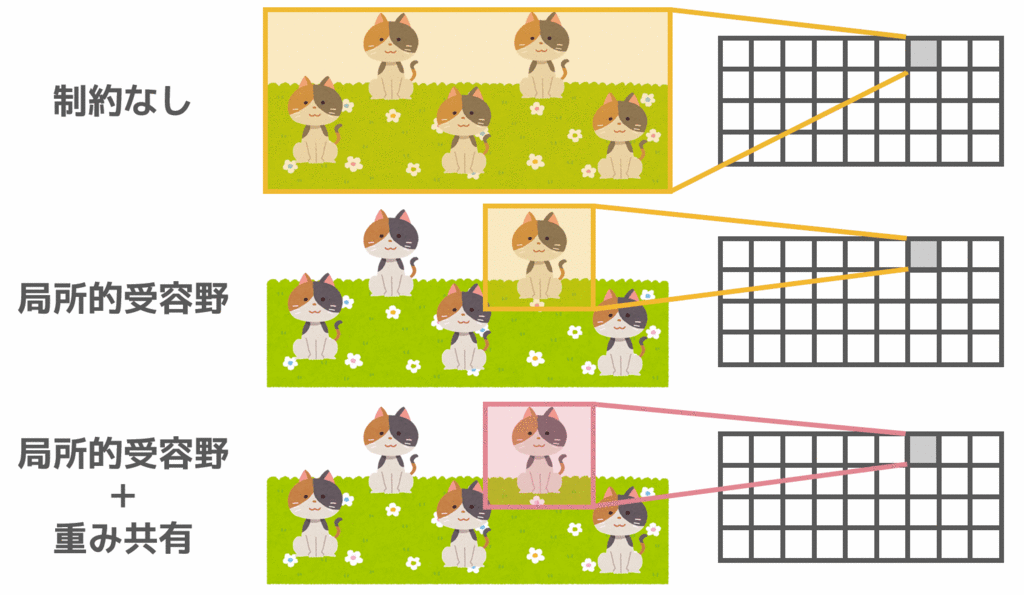
これで畳み込み層のおおよそのイメージを紹介しましたので、最初に示したより具体的な画像に戻ります。局所的受容野・重み共有が適用されていることが分かります。

畳み込み層の設定
畳み込み層には、フィルタの大きさやフィルタをずらす距離など、学習前に設定しなくてはいけないパラメータがあります。このように、学習を行う前に事前に設定するパラメータを、ハイパーパラメータといいます。
畳み込み層の設定を行うハイパーパラメータには、以下のようなものがあります。それぞれのハイパーパラメータについて、以下で説明を行います。
- チャンネルの枚数(入力と出力それぞれ必要)
- フィルタサイズ(フィルタの大きさ)
- ストライド(フィルタをずらす距離)
- パディング(余白の大きさ)
チャンネルの枚数
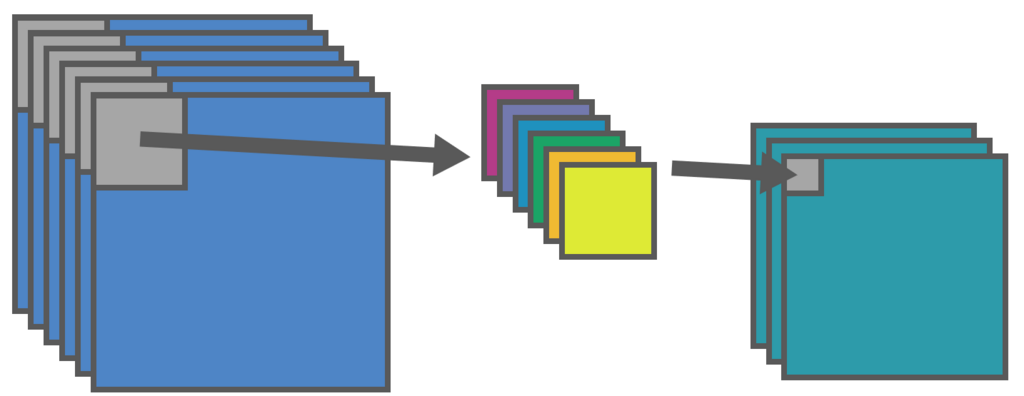
ここまでは、入力と出力ともにチャンネルの枚数が1枚でした。フィルタは入力と出力のチャンネルのペアごとに1枚必要なので フィルタの枚数 = 入力チャンネル数 × 出力チャンネル数 となります。
下図は、6枚のチャンネルから1枚のチャンネルへ出力を行っている図です。各チャンネルを対応するフィルタで畳み込みした値の合計が、1枚の出力チャンネルの値となります。
ストライド
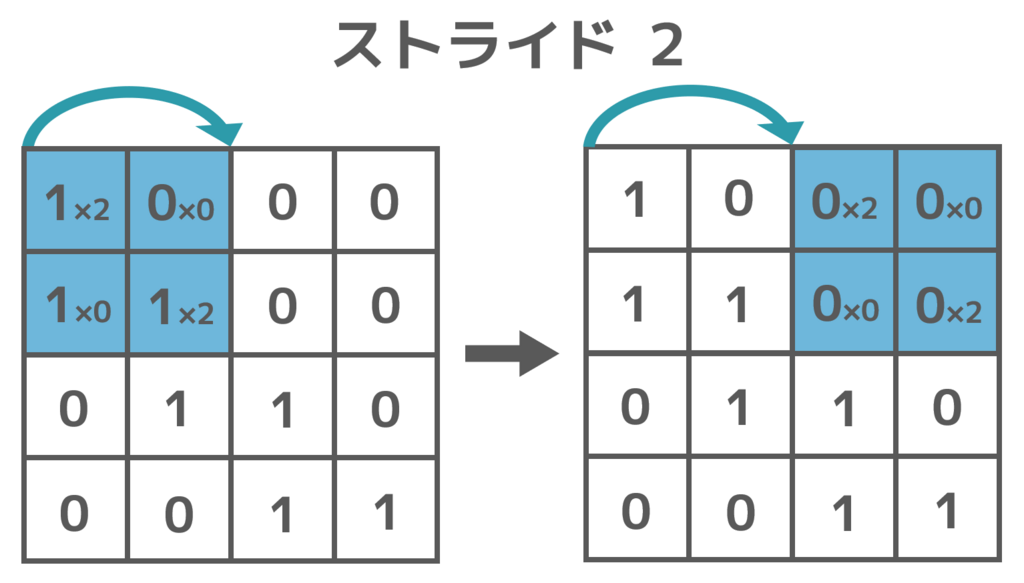
ストライドとは、フィルタをずらす距離のことです。下図のようにストライドが1のときは1マスずつずらし、ストライドが2のときは2マスずつずらします。

パディング
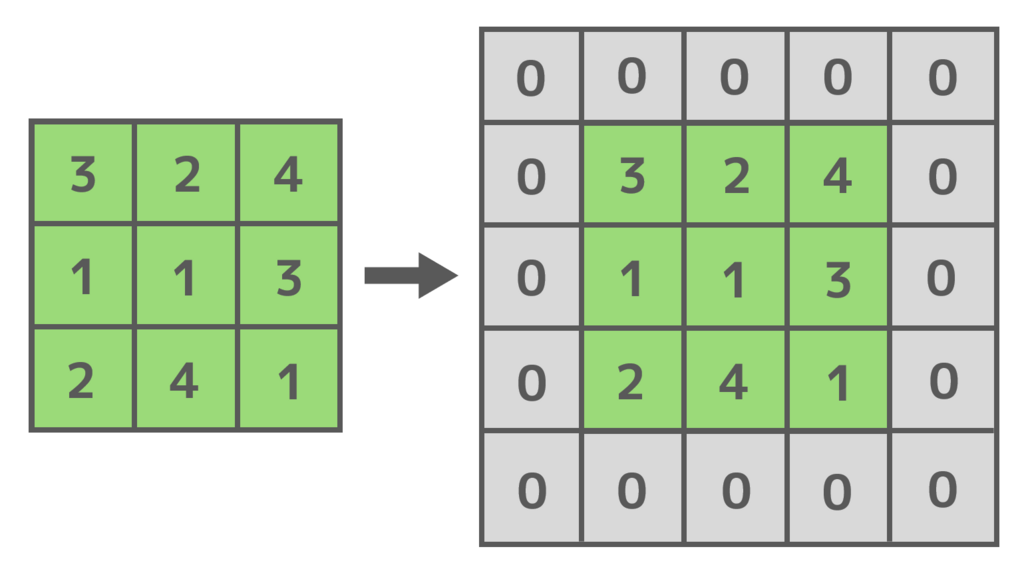
パディング(ゼロパディング)とは、畳み込みを行う前に入力チャンネルの周囲を0で埋めることです。これによって、畳み込み前と後のチャンネルの大きさを同じにすることが出来ます。
畳み込み層を数式で表現
ここまで、畳み込み層を図で表現してきました。畳み込み層の説明の最後に、畳み込み層を図ではなく数式で表現します。
畳み込み層を数式で表現すると以下のようになります。
:出力チャンネルの枚数
:入力チャンネルのサイズ
:ストライド
:フィルタの左上を重ねる場所の行番号と列番号
:
枚目の
行
列目の入力チャンネルの値
:p行q列目の, k番目の入力チャンネルからm番目の出力チャンネルへの値
:k枚目のi行j列目の出力チャンネルのバイアス
:
枚目の
行
列目の出力チャンネルの値
:活性化関数
\begin{align} y_{i,j,m} &= f(\sum_{k = 0}^{K - 1} \sum_{p,q=0}^{H-1} (w_{p,q,k,m} x_{Si+p, Sj+q, k} + b_{i,j,m})) \end{align}
KelpNetで畳み込み層を用いる
KelpNetでは、畳み込み層はConvolution2Dという名前でFunctionクラスとして実装されています。基本的には、入力チャンネルの数・出力チャンネルの数・カーネルサイズ(フィルタサイズ)・関数の名前を指定して使用します。それ以外のパラメータを指定したい場合は、定義する際に指定したいパラメータにのみ値を代入します。
- Convolution2D (inputChannels, outputChannels, kSize, stride = 1, pad = 0, noBias = false, initialW = null, initialb = null, name = FUNCTION_NAME, gpuEnable = false)
// 重みの初期値 Real[,,,] initial_W = { {{{1.0, 0.5, 0.0}, { 0.5, 0.0, -0.5}, {0.0, -0.5, -1.0}}}, {{{0.0, -0.1, 0.1}, {-0.3, 0.4, 0.7}, {0.5, -0.2, 0.2}}} }; // バイアスの初期値 Real[] initial_b = { 0.5, 1.0 }; // ネットワークの定義 FunctionStack model = new FunctionStack( // pad=1の場合 new Convolution2D(1, 2, 3, name="Conv2D") // パディングを指定する場合 new Convolution2D(1, 2, 3, pad: 2, name: "Conv2D") // GPUを用いる場合 new Convolution2D(1, 2, 3, name: "Conv2D", gpuEnable: true) // 重みとバイアスの初期値を指定する場合 new Convolution2D(1, 2, 3, initialW: initial_W, initialb: initial_b, name: "Conv2D") );
プーリング層
畳み込みニューラルネットワークは、畳み込み層とともにプーリング層を用いる場合があります。プーリング層では、チャンネルの各領域の値を1つの値にまとめます。これによって、局所的な特徴の位置のずれに対して頑健になる・過学習を抑制するなどの効果があります。
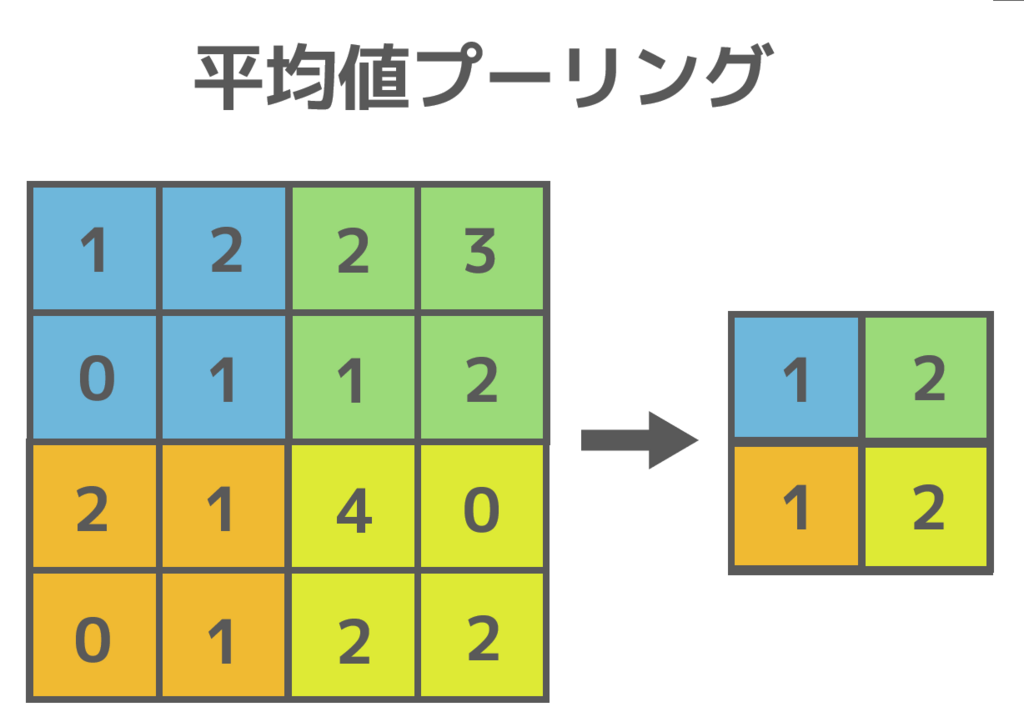
代表的なプーリングの手法には、平均値プーリング (average pooling) や 最大値プーリング (max pooling) などがあります。平均値プーリングは各領域の値の平均値を出力とし、最大値プーリングは各領域の値の最大値を出力とします。
下図はプーリングの例です。色分けされているものが、各領域です。青・緑・オレンジ・黄色の領域があります。平均値プーリングでは各領域での平均値を求め、最大値プーリングでは各領域での最大値を求めていることが分かります。

プーリング層の設定
プーリングの設定を行うハイパーパラメータには、以下のようなものがあります。それぞれのハイパーパラメータは畳み込み層と同様のもので、こちらで紹介しています。
- フィルタサイズ(領域の大きさ)
- ストライド(フィルタをずらす距離)
- パディング(余白の大きさ)
KelpNetでプーリング層を用いる
KelpNetでは、平均値プーリングはAveragePooling、最大値プーリングはMaxPoolingという名前でFunctionクラスとして実装されています。カーネルサイズ(フィルタサイズ)・関数の名前を指定することで使用出来ます。それ以外のパラメータを指定したい場合は、定義する際に指定したいパラメータにのみ値を代入します。
- AveragePooling (ksize, stride=1, pad=0, name=FUNCTION_NAME, gpuEnable=false)
- MaxPooling (ksize, stride=1, pad=0, name=FUNCTION_NAME, gpuEnable=false)
- AveragePoolingと同じ
// ネットワークの定義 FunctionStack model = new FunctionStack( new AveragePooling(2, 2, name: "AVEPooling") // 各パラメータを設定する場合 new AveragePooling(2, 2, stride=2, pad=1, name: "AVEPooling") // GPUを使用する場合 new AveragePooling(2, 2, name: "AVEPooling") );